Design beam to column Flange moment connections by CET.Calculator

Introduction #

In previous article, we talked about how to design a beam to column flange, single plate connection by the Connection Calculator at CET.Calculator. This article will show a more complicate case, to design beam to column flange moment connections. The beam web to column is using single plate connection and the beam flange to column is using flange plate connection. This example is from AISC Design 14th Example IIB-1. One important thing for the Connection Calculator is that it will only calculate one connection each time. For example, users will calculate beam web single plate connection and then calculate beam flange plate connection. However, CET.APIs (pyCET) could work on both connections at the same time and it is much more powerful.

Again, since we will use Typora to create PDF report, user could download Typora and add following lines to resources/window.html in Typora directory, to align equation to the left and show nice equations/outputs.

window.MathJax = {
  ....
  svg: {
    displayAlign: 'left',
    scale: 0.9,
    minScale: 80,
  },
...
};

Data Input #

For both web and flange connections, each one will have 20+ input items to get things done. To shorten this article , for the beam web connection (under shear load), users could copy beam web connection data (left to the following picture) and paste them to the left/top panel of the Connection Calculator, “Parameters” tab. Now all calculations about beam web connection will be shown. Note:

• “Check loads” in “Configuration” tab is for shear load.
• “Moment” will not be used in this calculation.
• After pasting the data, the “Connection type” in “Connection” tab changes to “Single Plate“.

After the web connection is done, users could copy and paste the beam flange connection data (left to the following picture) to “Parameters” tab again, to work on the flange plate connection. Note:

• Moment, 2016 kips-in, will be used. The forces in beam flange check and flange plate check will be calculated by the program.
• After pasting the data, the “Connection type” in “Connection” tab changes to “Flange Plate“.

Report #

Before start, users could create a new file in Typora and copy/paste following lines:

### 1 Summary
This the AISC 14th Design Example IIB-1 report generated by the **Connection Calculator** in **CET.Calculators**.

Given:
Design a bolted flange-plated FR moment connection between an ASTM A992 W18X50 beam and an ASTM
A992 W14X99 column flange to transfer the following vertical shear forces and strong-axis moments:

$V_D$ = 7.0 kips $M_D$ = 42 kip-ft
$V_L$ = 21 kips $M_L$ = 126 kip-ft

Use 0.875 in. diameter ASTM A325-N or F1852-N bolts in standard holes and 70-ksi electrodes. The flange plates
are ASTM A36 material. Check the column for stiffening requirements.

Using ASD design method

$R_a$ = 28.0 kips $M_a$ = 168 kip-ft

![examp](https://user-images.githubusercontent.com/100242816/163437243-8467e055-8409-4879-b1f7-3b18da51f314.JPG)

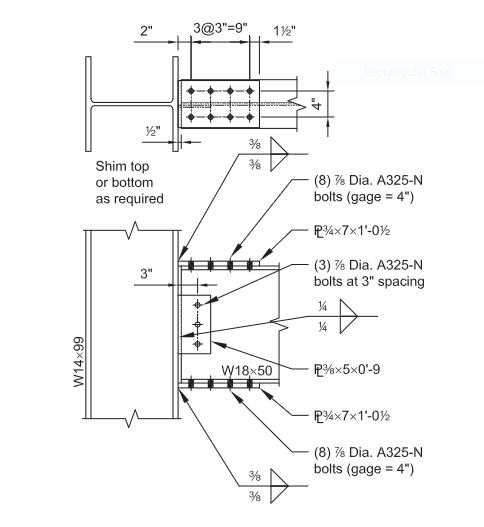
#### Strength Table
Beam Web
| Limit State    | Design Value | Check value | Ratio | Check Result | Reference  |
| -------------- | ------------ | ----------- | ----- | ------------ | ---------- |
| Shear Yielding |              |             |       |              | AISC G2    |
| Hole Bearing   |              |             |       |              | AISC J3.10 |

Beam Web Connection
| Limit State    | Design Value | Check value | Ratio | Check Result | Reference  |
| -------------- | ------------ | ----------- | ----- | ------------ | ---------- |
| Bolt Shear     |              |             |       |              | AISC J3.2  |
| Shear Yielding |              |             |       |              | AISC J4.2  |
| Shear Rupture  |              |             |       |              | AISC J4.2  |
| Block Shear    |              |             |       |              | AISC J4.3  |
| Hole Bearing   |              |             |       |              | AISC J3.10 |
| Welds          |              |             |       |              | AISC J2    |

Beam Flange
| Limit State  | Design Value | Check value | Ratio | Check Result | Reference  |
| ------------ | ------------ | ----------- | ----- | ------------ | ---------- |
| Block Shear  |              |             |       |              | AISC J4.3  |
| Hole Bearing |              |             |       |              | AISC J3.10 |
| Hole Reductions|              |             |       |              | AISC F13 |

Beam Flange Connection
| Limit State      | Design Value | Check value | Ratio | Check Result | Reference  |
| ---------------- | ------------ | ----------- | ----- | ------------ | ---------- |
| Bolt Shear       |              |             |       |              | AISC J3    |
| Tensile Yielding |              |             |       |              | AISC J4.1  |
| Tensile Rupture  |              |             |       |              | AISC J4.1  |
| Block Shear      |              |             |       |              | AISC J4.3  |
| Hole Bearing     |              |             |       |              | AISC J3.10 |
| Plate Buckling   |              |             |       |              | AISC J? |
| Welds            |              |             |       |              | AISC J2 |

### 2 Beam web check

### 3 Beam web connection check

### 4 Beam flange check

### 5 Beam flange plate connection check

### 6 Column check

Now, users could paste the beam web connection data to the “Parameters” tab again to get the calculation details about beam web. Then changing the display mode from Standard mode and Markdown mode (right to calculator list). In the right panel of the Connection Calculator,

1. Choose “Member” tab and copy everything to Typora document, under “### 2 Beam web check” section.
2. Choose “Connection” tab and copy everything to Typora document, under “### 3 Beam web connection check”. After this, The report of beam web connection is ready.

For beam flange calculation, users could:

1. Copy/paste the beam flange connection data to the “Parameters” tab again
2. Choose “Member” tab and copy/paste text to “### 4 Beam flange check” section
3. Choose “Connection” tab and copy/paste text to “### 5 Beam flange plate connection check” section
4. In the left panel of the Connection Calculator, “Member” tab, change “Check member” to “Column“
5. In the right panel of the Connection Calculator, choose “Member” tab and copy/paste text to “### 6 Column check” section. This part is about column capacities check and will be used for the design of column reinforcements, like transverse plates

Last step for users is to fill the capacity table and calculate the unity ratio (you can mark the maximum one). Though there are many steps to do, finally we can use Typora to create a 9 page PDF report by following  “File -> Export -> PDF” . The final PDF version is here.

Users will notice that some complicate calculations have been done by CET.Calculators. For example, the 3 cases block shear (L shape, 2l shape and U shape) for the flange plate has been calculated as followings, which greatly saved user’s time.

 Compare with AISC 14th Design Example IIB-1 #

The compare of CET.Calculator and AISC 14th Example IIB-1 is in following table

Check part	Check item	CET.Calculator	AISC 14th Example IIB-1	Difference
Beam web	Shear yield	127.8 kips	N/A
	Hole bearing	48.7 kips	N/A
Single plate (in beam web)	Bolt shear	48.71 kips	29.9 kips	See note (1)
	Shear yield	48.6 kips	48.6 kips	0
	Shear rupture	39.2 kips	39.2 kips	0
	Hole bearing	59.1 kips	N/A
	Block shear	46.69 kips	46.7 kips	0
	Weld	66.8 kips	66.8 kips	0
Beam flange	Block shear	196.4 kips	197 kips	0.3 %
	Hole bearing	279.3 kips	N/A
	Hole reduction	2537 kip-in.	2532 kip-in	0.2 %
Flange plate (in beam flange)	Bolt shear	129.9 kips	129.6 kips	0
	Tensile yield	113.2 kips	113 kips	0
	Tensile rupture	108.8 kips	109 kips	0
	Block shear, L shape	172.1 kips	172 kips	0
	Block shear, 2l shape	213.6 kips	213 kips	0.28 %
	Hole Bearing	327.9 kips	N/A
	Plate bucking	113.2 kips	113.2 kips	0
	Weld	116.9 kips	117 kips	0
Column capacity	Flange bending	113.6 kips	114 kips	0
	Web local yielding	123.7 kips	124 kips	0
	Web crippling	154.8 kips	155 kips	0

Note:

1. AISC 14th Example IIB-1 considers bolt group eccentricity for beam to column moment connection. According to AISC 14th page 12-3, for FR moment connection, we ignore the eccentricity.
2. We don’t list bearing calculations for AISC Example in above table, since we separate the bolt bearing check with bolt shear check.
3. We consider the beam underrun (0.25″) in calculations, the same as AISC example.

Conclusion #

1. The Connection Calculator is most complicate and powerful one in CET.Calculators. This article is showing how to design a beam to column, moment connection.
2. CET.Calculators could generate Markdown format text, which could be used by users to create professional report (including math equations).

The calculations of column transverse stiffener is coming soon ……